Before jumping into Prime Number Program in Java or how to check whether the given number is prime or not, let’s see what is a Prime number?
In Mathematics a Prime number is defined as a number that has no factors except 1 and the number itself. In other words, a number only divisible by one, and the number itself is called a Prime number.

The Java program for Prime number can be written in several ways. First, let’s try to implement the definition itself.
Prime Number Program in Java – Code
public class PrimeCheck{
public static void main(String args[]){
int i,flag=0;
int n=3;//it is the number to be checked
if(n==0||n==1){
System.out.println(n+" is not prime number");
}else{
for(i=2;i<n;i++){ //loop runs for i: 2 -> n-1
if(n%i==0){
System.out.println(n+" is not prime number");
flag=1;
break;
}
}
if(flag==0) { System.out.println(n+" is prime number"); }
}//end of else
}
} OUTPUT
3 is prime numberIn the above code, we run a loop from 2 to (n-1) and check if any number divides the given number.
If so then the number is not a Prime number and we set the flag as 1 and terminate the loop with a break statement.
This code works fine. But with the time complexity of O(n). A common idea to reduce this is by running the loop till (n/2). This also works BUT here’s what I think is the best solution for this problem.
BETTER WAY TO CHECK FOR PRIME NUMBER IN JAVA-
public class PrimeCheck2{
public static void main(String args[]){
int n=37;//it is the number to be checked
if(n == 2 || n == 3 || n ==5 || n == 7) {
System.out.println(n +" is a Prime Number!");
return;
}
if(n%2 != 0 && n%3 != 0 && n%5 != 0 && n%7 != 0)
System.out.println(n +" is a Prime Number!");
else
System.out.println(n +" is not a Prime Number!!");
}
} OUTPUT
37 is prime number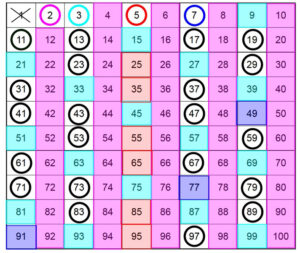
Here we follow the idea that if the given number is 2 or 3 or 5 or 7 then it is prime straight away. Otherwise, we see if the number is not divisible by 2 or 3 or 5 or 7, if so then again it is a Prime or else not. This algorithm is also known as the Sieve of Eratosthenes. All Prime Numbers until a given range can be found using this idea.
Time complexity: O(1) [no iteration required]
Java Program for Prime Numbers using Recursion:
Though not the best way, Prime number check can be a good program to practice recursion and understand its usage. Here we create an IsPrime function with boolean return type- true if Prime: false if not. Here the recursion continues till the divisor i is greater than the square root of the given number.
CODE
public class helloWorld{
static boolean isPrime(int n, int i) // call method with i as 2.
{
// Base cases
if (n <= 2) return (n == 2) ? true : false;
if (n % i == 0) return false;
if (i * i > n)
return true;
// Check for next divisor
return isPrime(n, i + 1);
}
public static void main(String args[]){
int n=39;//it is the number to be checked
if(isPrime(n, 2)) {
System.out.println(n +" is a Prime Number!");
}
else
System.out.println(n +" is not a Prime Number!!");
}
} OUTPUT
39 is not a Prime Number!!