In Java Graph Data Structure, we shall learn how to build a Graph and operate it from scratch. A graph is a non-linear data structure consisting of nodes and edges.
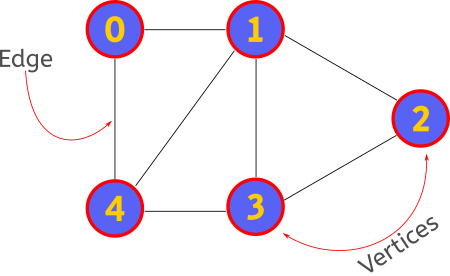
Graph Representation in Java
The above graph has 5 vertices named from 0 to 4. Now the question arises, how to create a graph to operate within our code? Basically, there are 2 ways to demonstrate a Graph.
Graph Java Implementation
Using-
- adjacency-list
- adjacency-matrix
Adjacency List: A graph is represented as an array of the linked list. The index of the array represents a vertex and each element in its linked list represents the vertices that form an edge with the vertex. The following image represents the adjacency list representation:

adjacency list java
Java Graph Class Code
All our methods are created in GraphDemo class. These global declarations are used in our code:
public class GraphDemo {
int n; // number of nodes
int adjmat[][];
List adjlist[];
GraphDemo(int n){
adjmat = new int[n][n];
adjlist = new ArrayList[n];
this.n = n;
}In this method, we use an array of ArrayList to add the nodes connected for each node. We have used the number to character conversion following ASCII code to print the Graph nodes. 65-90 represents A-Z. At the same time, we avoid questions like if the same nodes are connected?
void createList() {
Scanner sc = new Scanner(System.in);
for(int i=0; i<n; i++) {
List addlist = new ArrayList();
for(int j = 0; j<n; j++) {
if(i == j) // to skip questions like: are A and A connected?
continue;
System.out.print("Are "+(char)(65+i)+" and "+(char)(65+j)+" connected? 1-YES/ 0-NO : ");
int inp = sc.nextInt();
if(inp == 1)
addlist.add((65+j));
}
adjlist[i] = addlist;
}
sc.close();
}
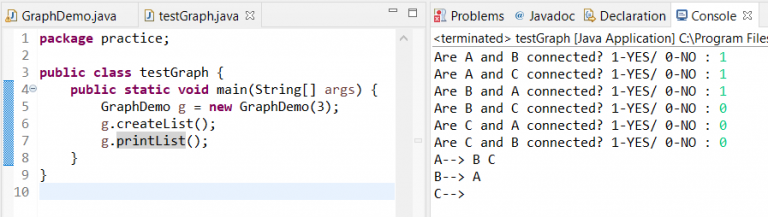
Output of Java graph
Adjacency Matrix: Here, a graph is represented in the form of a two-dimensional array. The size of the array is V x V, where V is the set of vertices. The following image represents the adjacency matrix representation:

Adjacency Matrix Java
Adjacency Matrix Java code
This is the method used to populate the matrix for graph representation.
void createMatrix() {
Scanner sc = new Scanner(System.in);
for(int i=0; i<n; i++) {
for(int j=0; j<n; j++) {
if(i == j) // to skip questions like: are A and A connected?
continue;
System.out.print("Are "+(char)(65+i)+" and "+(char)(65+j)+" connected? 1-YES/ 0-NO : ");
int inp = sc.nextInt();
if(inp == 1) {
adjmat[i][j] = 1;
}
}
}
sc.close();
}
Output
We have used a print Matrix method to print the output in a readable manner.
void printMatrix() {
for(int i=0; i<n; i++) {
if(i == 0) {
System.out.print(" ");
for(int m = 0; m < n; m++) {
System.out.print((char)(65+m)+" ");
}
System.out.println();
}
for(int j=0; j<n; j++) {
if(j == 0) {
System.out.print((char)(65+i)+" ");
}
System.out.print(adjmat[i][j]+" ");
}
System.out.println();
}
}Java Graph Data Structure Algorithms
The basic algorithm is about how to search in a graph?
The two main methods are Depth-First Search(DFS) and Breadth-First Search(BFS).
We have implemented both these methods using an adjacency matrix. The same will be possible using the adjacency list. In fact, using a list will be more efficient as we shall not be iterating through cases where there are no connections at all.
Now we shall study each of them in details:
Depth-First Search Java
In DFS the concept is that we shall dive as deep as possible in the graph and print each node as we visit them. Technically we use a stack to achieve this order.
void DFS(int v) {
if(v > n) {
System.out.println("node "+v+" exceeds limit! max: "+n);
return;
}
int visited[] = new int[n];
System.out.print("DFS: ");
DFSUtil(visited,v);
}
void DFSUtil(int visited[], int v) {
if(visited[v] == 1)
return;
visited[v] = 1;
System.out.print((char)(65+v)+" ");
for(int i=0; i<n; i++) {
if(adjmat[v][i] == 1) {
DFSUtil(visited,i);
}
}
}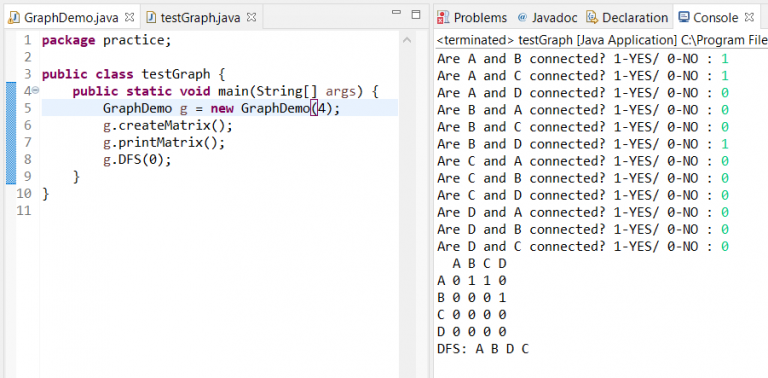
DFS Java Output
In the above output, we have entered a graph with 4 nodes – A, B, C, and D. A is connected to B and C. D is connected to B only. We start the search from node A, move to B then D. Every time we update the visited array so that we don’t revisit any node. Since the D node has no connections, the control returns to the next connection of Node A, that is C.
Breadth-First Search Java
In this algorithm, we start from any node and traverse the adjacent nodes. Similarly proceeding to the next node and traverse all the adjacent nodes. It is quite similar to level-order traversal in trees. Only we keep a record of the nodes visited so that we don’t revisit any node.
void BFS(int v) {
if(v > n) {
System.out.println("node "+v+" exceeds limit! max: "+n);
return;
}
int visited[] = new int[n];
System.out.print("BFS: ");
BFSUtil(visited,v);
}
private void BFSUtil(int[] visited, int v) {
Queue q = new LinkedList();
q.add(v);
visited[v] = 1;
while(true) {
for(int i=0; i<n; i++) {
if(adjmat[v][i] == 1) {
if(visited[i] == 1)
continue;
visited[i] = 1;
q.add(i);
}
}
if(!q.isEmpty()) {
System.out.print((char)(65+q.poll())+" ");
if(q.isEmpty())
break;
v = q.peek();
}
}
}
Output Breadth-First Search implementation Java
Here, we push all the connections of starting node(node-A) in a queue. Then we pop the head of the queue and in the next iteration, we search the connections of this node. In this way, we print the starting node, followed by all its connection node and their connections after them.
We hope this tutorial helped you to achieve the same. Keep learning keep sharing. Follow us on Facebook and Instagram.
Nice content
I am looking for a small help related to my assignment. Let me know how can I contact you guys.