Binary Tree Java | Complete Guide with Code Example

A Java Binary Tree is a non-linear data structure where data objects are organized in terms of hierarchical relationships.

Every value in the tree is a node. The first value 6 has 2 child nodes 4 and 8. 4 and 8 again have 2 child nodes each.

In general, a Binary Tree has no conditions for new insertion but a Binary Search Tree will follow a definite order.

The above example is also a BST(Binary Search Tree).

Here, we shall also take care that every left child of a node is smaller than the node itself and the right child is greater. This later helps in several types of search implementations.

Let’s say we want to find the smallest value in a BST, then we simply move left from the root node(6) until we hit end(node 3).

How easy!

Java Binary Tree Implementation

First, we define a class named TreeNode for every node in the Tree.

This class will contain the value, the left, right child, and also the parent node.

//defining a TreeNode class with data, parent, left and right child
	private class TreeNode{
		int data;
		TreeNode parent;
		TreeNode left;
		TreeNode right;
		public TreeNode(int data, TreeNode parent) {
			this.data = data;
			this.parent = parent;
		}
		public TreeNode() {
			// TODO Auto-generated constructor stub
		}
	}

Now, we must define the necessary functions to work with our Binary Search Tree.

The basic operations are:

1. add
2. traversal
3. delete.

Let’s look at them one at a time.

add:

In this method, we pass a tree node and its parent node and the new value.

• At first, we check if the head is null?
• Then we create a head node.
• Else we compare the new node value with the current node value.
• If the new node value is less than the current node then we make a recursive call with the left node of the current node in line 13.
• Before that, we must make sure that the left node is null.
• Similarly, the right child node is called if the new node is larger than the current node.

void addUtil(TreeNode t, TreeNode parent, int value) {

		if (head == null) {
			head = new TreeNode(value, parent);
			//System.out.println(" "+head.data);
		}
		else {
			if(t.data > value) {
				if(t.left == null) {
					t.left = new TreeNode(value,t);
					return;
				}
				addUtil(t.left,t,value);
			}
			else {
				if(t.right == null) {
					t.right = new TreeNode(value,t);
					return;
				}
				addUtil(t.right,t,value);
			}
		}
	}

traversal:

We can traverse a BST in four primary ways

1. InOrder
2. PreOrder
3. PostOrder
4. LevelOrder

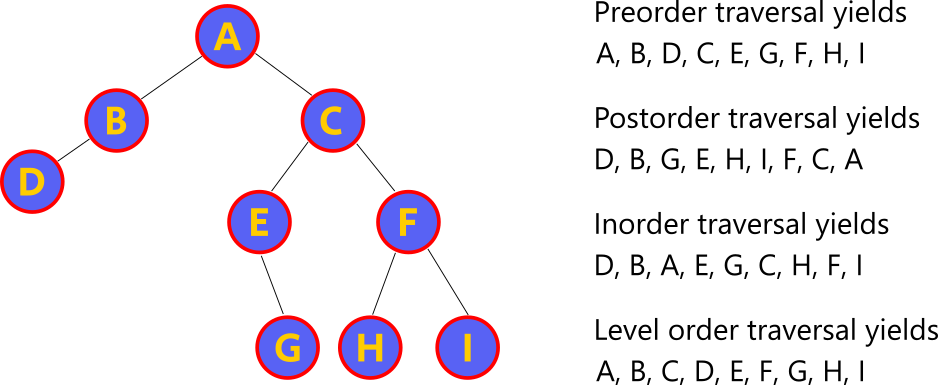
Preorder, Postorder, Inorder, Level order traverse a BST in primary ways

InOrder

Here, we make a recursive call to the left child. Then print the current node value and again make a recursive call with the right child.

void inorderUtil(TreeNode t, int i) {
		i++;
		if(t == null)
			return;
		inorderUtil(t.left, i);
		System.out.print(" "+t.data);
		inorderUtil(t.right, i);
		if(i == 1)
			System.out.println();
	}

You can ignore the value i. As its sole purpose is to move to the next line after traversing the tree.

PreOrder

In this traversal, we visit every node and print it first. Then we make two sequential recursive calls with left and right children.

void preorderUtil(TreeNode t, int i) {
		i++;
		if(t == null)
			return;
		System.out.print(" "+t.data);
		preorderUtil(t.left, i);
		preorderUtil(t.right, i);
		if(i == 1)
			System.out.println();
	}

PostOrder

First, we make the recursive calls and then we print the node value in the end.

void postorderUtil(TreeNode t, int i) {
		i++;
		if(t == null)
			return;
		postorderUtil(t.left, i);
		postorderUtil(t.right, i);
		System.out.print(" "+t.data);
		if(i == 1)
			System.out.println();
	}

LevelOrder

We traverse the tree each level at a time. For this one, we also need a maxHeight function to calculate the height of the Binary Tree.

int maxHeight(TreeNode t) {
		if(t == null)
			return 0;
		else {
			int lheight = maxHeight(t.left);
			int rheight = maxHeight(t.right);
			if(lheight > rheight)
				return lheight+1;
			else
				return rheight+1;
		}
	}
	void levelorder() {
		System.out.print("levelorder: ");
        int height = maxHeight(head);
        for(int i = 1; i<=height; i++)
        	levelorderUtil(head, i);
		System.out.println();
	}
	void levelorderUtil(TreeNode t, int lvl) {
		if(t == null)
			return;
		else if(lvl == 1)
			System.out.print(t.data+" ");
		else {
			levelorderUtil(t.left, lvl-1);
			levelorderUtil(t.right, lvl-1);
		}

	}

delete:

Let’s say we want to delete a Treenode from our tree. We shall face 3 distinct situations, the node to be deleted having –

1. no child
2. one child
3. two child

In the case of no child, we don’t have anything to take care of. We simply delete the required node.

In case 2, for one child, we delete the connection of the node with its parent by establishing a connection between its parent and child.

In the last case, for 2 children, the complexity arises. Here, we search for the maximum in the left sub-tree and update the value of the node to be deleted with it. Then we again call the function to delete the Maximum value in the left-subtree because now our tree has a duplicate of that node in place of the node to be deleted.

void delete(int value) {
		if(findNode(head, value)) {
			System.out.println("deleted node "+value);
		}
		else {
			System.out.println("node "+value+" not found! ");
		}
	}
	boolean findNode(TreeNode t, int value) {
		while(t != null) {
			if(t.data > value) {
				t = t.left;
			}
			else if(t.data < value){
				t = t.right;
			}
			else {
				//delete
				deleteUtil(t,t.parent,value);
				return true;
			}

		}
		return false;
	}
	void deleteUtil(TreeNode t,TreeNode p, int value) {
		//2 child
		if(t.left != null && t.right != null) {
			t.data = findMax(t.left);
			deleteUtil(t.left, t, t.data);
		}
		//no child
		else if(t.left == null && t.right == null) {
			if(p.left.data == t.data) {
				p.left = null;
			}
			else {
				p.right = null;
			}
		}
		//1 child
		else {
			TreeNode temp = t.left == null ? t.right : t.left;
			if(p.left.data == t.data) {
				p.left = temp;
			}
			else {
				p.right = temp;
			}
		}
	}
	int findMax(TreeNode t) {
		if(t.right != null) {
			t = t.right;
		}
		return t.data;
	}

Code Java Binary Tree Example

BST.java

public class BST {
	TreeNode head;
	
	//defining a TreeNode class with data, parent, left and right child
	private class TreeNode{
		int data;
		TreeNode parent;
		TreeNode left;
		TreeNode right;
		public TreeNode(int data, TreeNode parent) {
			this.data = data;
			this.parent = parent;
		}
	}
	
	//insertion of node in BST
	void add(int value) {
		addUtil(head,null,value);
	}
	void addUtil(TreeNode t, TreeNode parent, int value) {

		if (head == null) {
			head = new TreeNode(value, parent);
			//System.out.println(" "+head.data);
		}
		else {
			if(t.data > value) {
				if(t.left == null) {
					t.left = new TreeNode(value,t);
					return;
				}
				addUtil(t.left,t,value);
			}
			else {
				if(t.right == null) {
					t.right = new TreeNode(value,t);
					return;
				}
				addUtil(t.right,t,value);
			}
		}
	}
	
	
	void inorder() {
		System.out.print("inorder: ");
		inorderUtil(head, 0);
	}
	void inorderUtil(TreeNode t, int i) {
		i++;
		if(t == null)
			return;
		inorderUtil(t.left, i);
		System.out.print(" "+t.data);
		inorderUtil(t.right, i);
		if(i == 1)
			System.out.println();
	}
	
	void preorder() {
		System.out.print("preorder: ");
		preorderUtil(head, 0);
	}
	void preorderUtil(TreeNode t, int i) {
		i++;
		if(t == null)
			return;
		System.out.print(" "+t.data);
		preorderUtil(t.left, i);
		preorderUtil(t.right, i);
		if(i == 1)
			System.out.println();
	}
	void postorder() {
		System.out.print("postorder: ");
		postorderUtil(head, 0);
	}
	void postorderUtil(TreeNode t, int i) {
		i++;
		if(t == null)
			return;
		postorderUtil(t.left, i);
		postorderUtil(t.right, i);
		System.out.print(" "+t.data);
		if(i == 1)
			System.out.println();
	}
	int maxHeight(TreeNode t) {
		if(t == null)
			return 0;
		else {
			int lheight = maxHeight(t.left);
			int rheight = maxHeight(t.right);
			if(lheight > rheight)
				return lheight+1;
			else
				return rheight+1;
		}
	}
	void levelorder() {
		System.out.print("levelorder: ");
        int height = maxHeight(head);
        for(int i = 1; i<=height; i++) levelorderUtil(head, i); System.out.println(); } void levelorderUtil(TreeNode t, int lvl) { if(t == null) return; else if(lvl == 1) System.out.print(t.data+" "); else { levelorderUtil(t.left, lvl-1); levelorderUtil(t.right, lvl-1); } } void print() { printUtil(head, 0, 0); } void printUtil(TreeNode t, int c, int lvl) {//left -> -1 right -> 1
		int shift = 20;
		if(t == null) {
			return;
		}
		for(int i = 0; i<c+shift; i++) { System.out.print(" "); } System.out.println(t.data); lvl += 2; printUtil(t.left, c-10+(lvl), lvl); printUtil(t.right, c+10-(lvl), lvl); } void delete(int value) { if(findNode(head, value)) { System.out.println("deleted node "+value); } else { System.out.println("node "+value+" not found! "); } } boolean findNode(TreeNode t, int value) { while(t != null) { if(t.data > value) {
				t = t.left;
			}
			else if(t.data < value){
				t = t.right;
			}
			else {
				//delete
				deleteUtil(t,t.parent,value);
				return true;
			}

		}
		return false;
	}
	void deleteUtil(TreeNode t,TreeNode p, int value) {
		//2 child
		if(t.left != null && t.right != null) {
			t.data = findMax(t.left);
			deleteUtil(t.left, t, t.data);
		}
		//no child
		else if(t.left == null && t.right == null) {
			if(p.left.data == t.data) {
				p.left = null;
			}
			else {
				p.right = null;
			}
		}
		//1 child
		else {
			TreeNode temp = t.left == null ? t.right : t.left;
			if(p.left.data == t.data) {
				p.left = temp;
			}
			else {
				p.right = temp;
			}
		}
	}
	int findMax(TreeNode t) {
		if(t.right != null) {
			t = t.right;
		}
		return t.data;
	}

}

testTree.java

public class testTree {
	public static void main(String[] args) {
		BST t = new BST();
		t.add(3);
		t.add(4);
		t.add(1);
		t.add(0);
		t.add(2);
		t.add(6);
		t.add(7);
		t.add(5);
		t.inorder();
		t.preorder();
		t.postorder();
		t.levelorder();
		t.print();
		t.delete(4);
		t.print();
	}
}

OUTPUT

Java Tree Library

Java also provides tree-based data structure implementations for us to use:

• TreeSet
• TreeMap

TreeSet

TreeSet is one of the most important implementations of the SortedSet interface in Java that uses a Tree for storage. The ordering of the elements is maintained by a set using their natural ordering. It can also be ordered by a Comparator provided at set creation time, depending on which constructor is used. The TreeSet implements a NavigableSet interface by inheriting AbstractSet class.

import java.util.*; 
  
class TreeSetExample { 
  
    public static void main(String[] args) 
    { 
        TreeSet ts1 = new TreeSet(); 
  
        // Elements are added using add() method 
        ts1.add("A"); 
        ts1.add("B"); 
        ts1.add("C"); 
  
        // Duplicates will not get insert 
        ts1.add("C"); 
  
        // Elements get stored in default natural 
        // Sorting Order(Ascending) 
        System.out.println(ts1); 
    } 
} 

TreeMap

Java TreeMap class is a red-black tree-based implementation. It provides an efficient means of storing key-value pairs in sorted order.

The important points about the Java TreeMap class are:

• Java TreeMap contains values based on the key. It implements the NavigableMap interface and extends AbstractMap class.
• Contains only unique elements.
• Java TreeMap cannot have a null key but can have multiple null values.
• Java TreeMap is non synchronized.
• Maintains an ascending order.

OUTPUT

import java.util.*;  
class TreeMapExample{  
	public static void main(String args[]){  
		TreeMap<Integer,String> map=new TreeMap<Integer,String>();    
		map.put(100,"Amit");    
		map.put(102,"Ravi");    
		map.put(101,"Vijay");    
		map.put(103,"Rahul");    

		for(Map.Entry m:map.entrySet()){    
			System.out.println(m.getKey()+" "+m.getValue());    
		}    
	}  
}  

OUTPUT

We hope this tutorial helped you to achieve the same. Keep learning keep sharing. Follow us on Facebook and Instagram. Also, if you need any Java homework help or Java coding help, feel free to contact us.