Recursion is not just limited to “Java Recursion”. It is a widely used fundamental concept in the world of programming. Are you struggling to understand what recursion is? Well, this is a complete guide to recursion Java.
What is Recursion?
Basically, a function that calls itself directly or indirectly. Let’s take a look at this example :
Equation: f(x) = f(x-1) + 1 | f(0)=1

A simple mathematical equation where the value of f(x) is dependent on f(x-1).
Now, let’s try to code it out in Java.
public class RecursionExample {
static int f(int x) {
if(x == 0)
return 1;
return f(x-1)+1;//recursive call
}
public static void main(String[] args) {
int x = 10;
for(int i=0; i<x; i++)
System.out.print("f("+i+") = "+f(i)+", ");
}
}Output
f(0) = 1, f(1) = 2, f(2) = 3, f(3) = 4, f(4) = 5, f(5) = 6, f(6) = 7, f(7) = 8, f(8) = 9, f(9) = 10,
Here, the function f(x) has been called in a loop with values from 0 to 9.
When called with 0 the if-block returns 1.
Next time when called with 1, the function returns f(1-1)+1 i.e f(0)+1.
Another call to the function f(x) with value 0. Which we already know returns 1.
Therefore, the value of f(1) will be 1+1 = 2. Similarly, f(2) will be f(1)+1and f(3) = f(2)+1.
Types of Java Recursion
Direct Recursion– As the name suggests, the function makes a direct recursive call when it calls itself within the function body. The above example would be an instance of direct recursion.
Indirect Recursion– In this case a function ‘A calls another function ‘B’. Which in some way calls back the function ‘A’. Imagine some sort of closed cycle of function calls. For instance, any cyclic process such as the water cycle.

Let’s write a java code to demonstrate the water cycle.
public class IndirectRecursion {
static int numberOfCycles = 2;
static int start = 1;
static int evaporation(int x) {
if(x > numberOfCycles) // base case
return 0;
System.out.println("***"+"cycle "+x+"***");
System.out.println("evaporation...");
return condensation(x);
}
static int condensation(int x) {
System.out.println("condensation..");
return precipitation(x);
}
static int precipitation(int x) {
System.out.println("precipitaion..");
return evaporation(++x);
}
public static void main(String[] args) {
evaporation(start);
}
}Output
***cycle 1***
evaporation...
condensation..
precipitaion..
***cycle 2***
evaporation...
condensation..
precipitaion..In the above example, we created a method evaporation(int x) to first check if x is more than the number of cycles.
If so, we return 0 and end the cycle. Else we call the method condensation(int x).
Which in turn calls precipitation(int x). In precipitation, we increase the x value by 1 and pass it to the evaporation method. Therefore, the cycle continues.
Tail Recursion Java– When the recursive call is the last statement in the function. This type 0f recursion is more efficient because it uses less memory and the function need not do any operations while returning. For instance,
public class TailRecursion {
static void rec(int x) {
if(x == 0)
return;
System.out.print(x+" ");
rec(--x); //recursive call
}
public static void main(String[] args) {
rec(3);
}
}Output
3 2 1 Head Recursion Java– When the recursive call is the first statement in the function block it is known as Head recursion. For example,
public class TailRecursion {
static void rec(int x) {
if(x > 0) {
rec(--x); //recursive call
System.out.print(x+" ");
}
}
public static void main(String[] args) {
rec(3);
}
}Output
0 1 2 Tree Recursion Java
Another type of recursion is Tree recursion. This needs to be explicitly mentioned for its wide use. Fibonacci, Merge Sort, Quick Sort and many more popular algorithms use Tree Recursion.
In a Tree recursion, more than one recursive call is made within the function. Therefore giving the call stack a tree-like structure.
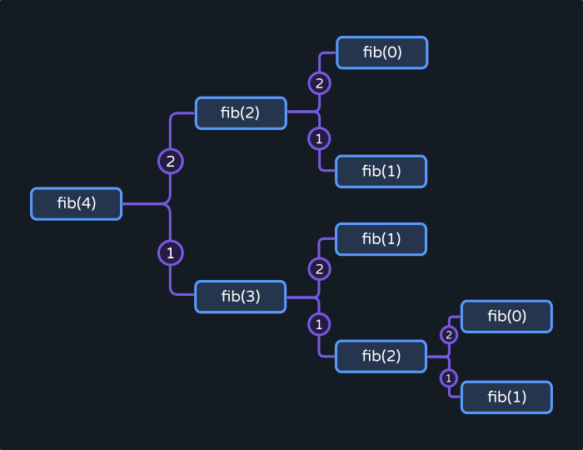
Simple Java Recursion Example
public class fibRec{
static int fib(int x) {
if(x < 2) //base case
return x;
return fib(x-1)+fib(x-2);
}
public static void main(String[] args)
{
for(int i = 0; i<5; i++) {
System.out.print(fib(i)+" ");
}
}
}Output
0 1 1 2 3 Find the minimum value in Array using Recursion Java
Now we have hovered over so many different types of recursion. Let’s dive into an example.
Here we shall attempt to find the smallest number in an array using recursion.
Any ideas? Go ahead and code it yourself.
Anyway, here’s a solution for help.
public class MinimumUsingRec {
static int findMinRec(int arr[], int n, int min) {
if(n == 0) //base case
return min;
if(arr[n-1] < min) {
min = arr[n-1];
}
return findMinRec(arr, n-1, min);
}
public static void main(String[] args) {
int arr[] = {5,2,3,4};
int n = arr.length;
System.out.println("minimum value: "+findMinRec(arr, n, Integer.MAX_VALUE));
}
}Output
minimum value: 2
In the above example the method findMinRec(int arr[], int n, int min) takes in 3 parameters.
An array arr[] and 2 integers n and min. n is the length of the array arr[]. min is the minimum value in the array arr[].
Now recursively we compare the elements in the array with the min value.
Therefore we pass the maximum value of an integer initially to the function at line 13 – Integer.MAX_VALUE.
When compared with arr[n-1] in line 5, the value gets updated.
Every recursive function must have a base case. The condition which will stop the recursion.
In this case, when the n value will be 0. Meaning that no more elements are left in the array.
Therefore, we must return the min value calculated so far. This min value will be the final output of the function.
Visualization
Called findMinRec(arr, n, min) with values:
arr=[5, 2, 3, 4] | n=4 | min=2147483647
n=4********************
arr[3]=4 < min=2147483647 ?
Yes! min=4
n=3********************
arr[2]=3 < min=4 ?
Yes! min=3
n=2********************
arr[1]=2 < min=3 ?
Yes! min=2
n=1********************
arr[0]=5 < min=2 ?
No!
n=0********************
base case true. Return answer...
minimum value: 2Code for visualization
public class MinimumUsingRec {
static int findMinRec(int arr[], int n, int min) {
System.out.println("n="+n+"********************");
if(n == 0) {// base case
System.out.println("base case true. Return answer...");
return min;
}
System.out.println("arr["+(n-1)+"]="+arr[n-1]+" < "+"min="+min+" ?");
if(arr[n-1] < min) {
min = arr[n-1];
System.out.println("Yes! min="+min);
}
else {
System.out.println("No!");
}
return findMinRec(arr, n-1, min);
}
public static void main(String[] args) {
int arr[] = {5,2,3,4};
int n = arr.length;
int min = Integer.MAX_VALUE;
System.out.println("Called findMinRec(arr, n, min) with values:");
System.out.println("arr="+Arrays.toString(arr)+" | n="+n+" | min="+min);
System.out.println("minimum value: "+findMinRec(arr, n, min));
}
}Can you guess the type of recursion here?
Yes! this is a tail-recursion. Since the recursive statement is the last line to execute in the function findMinRec(arr, n ,min).
Reverse String Java Recursion
In this problem, we shall be given an input String and we have to reverse the input string using a recursive function. There can be multiple solutions to this problem.
We will solve it using tail recursion again for its advantage over other types of recursion.
public class ReverseRec {
static String revString(String inp, String rev, int n) {
if(n == 0) // base case
return rev;
rev += inp.charAt(n-1);
return revString(inp, rev, n-1);// recursive call
}
public static void main(String[] args) {
String inp = "letstacle";
String rev = revString(inp, "", inp.length());
System.out.println("input - "+inp+" | reverse - "+rev);
}
}Output
input - letstacle | reverse - elcatstel
Here we have read the input String in reverse order and added it to the reverse String rev += inp.charAt(n-1);. When n is 0 it means that the entire string has been read. Therefore we have returned the reverse string as result.
Visualization
input - letstacle | reverse - e
input - letstacle | reverse - el
input - letstacle | reverse - elc
input - letstacle | reverse - elca
input - letstacle | reverse - elcat
input - letstacle | reverse - elcats
input - letstacle | reverse - elcatst
input - letstacle | reverse - elcatste
input - letstacle | reverse - elcatstel
input - letstacle | reverse - elcatstelCode for visualization
public class ReverseRec {
static String revString(String inp, String rev, int n) {
if(n == 0) // base case
return rev;
rev += inp.charAt(n-1);
System.out.println("input - "+inp+" | reverse - "+rev);
return revString(inp, rev, n-1);// recursive call
}
public static void main(String[] args) {
String inp = "letstacle";
String rev = revString(inp, "", inp.length());
System.out.println("input - "+inp+" | reverse - "+rev);
}
}Like this article? Follow us on Facebook and LinkedIn. You can also subscribe to our weekly Feed.