Trigonometry Questions and Answers

In this blog on trigonometry, we will solve some trigonometry questions and answers to brush up on our concept using identities.  Trigonometry is a combination of two Greek words- ‘Trigonon’ meaning a triangle and ‘metron’ meaning measure. In this blog, we will solve some of the problem statements to understand this concept better. Test your understanding of the practice problem and solve the step-by-step solution.

Solved Trigonometry questions

Problem 1: Find the length of the side unknown?

Solution :

x = \frac{20} {tan(45°)} = 20 

H = \frac{20} {sin(45°)} = 28.28

Problem 2:Find all sides of the right-angle triangle if the area of the is 625.

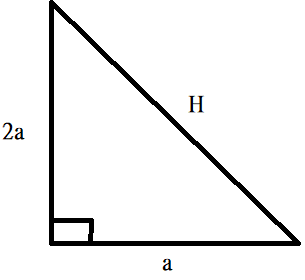
Solution:

Here, area of a triangle =\frac{1}{2}base *height

Area of triangle=\frac{1}{2} (2a)(a) = 625

So, a = 25 , 2a = 50

Using Pythagoras’s theorem
(opp.)^2 + (adj.)^2 = (Hypo.)^2 \\

(2a)^2 + (a)^2 = H^2

H = a √(5)= 25 √(5)

Problem 3:Find the length if DB is perpendicular to AB.

Solution :

Given AC perpendicular to DB means that triangles ACD and ACB are right triangles.
Hence,
\ tan (30°) = \frac {10} {AC} or AC = \frac {10} {tan (30°)}

BC = 20 – AC = 19 - \frac {10} {tan (30°)}

Pythagoras’s theorem applied to right \triangle ACB:
11^2 + BC^2 = x^2

solve for x and substitute BC: x = \sqrt ([ 10^2 + (20 - \frac {10} {tan (30°)})^2 )

= 107.12 (rounded to 3 significant digits)

Problem 4: Find the value of \tan \theta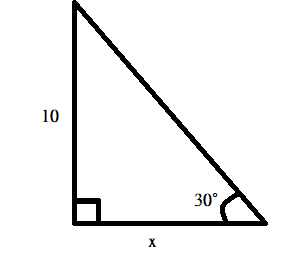
Solution :

We have the opposite side (O) =10 and Adjacent side = x

\tan \theta =\frac{opposite}{adjacent}

\tan 30= \frac{10}{x}

x=\frac{10}{\ tan 30}

x= 17.33

Problem 5: Solve 2 \tan(\theta)- \cot(\theta)=-1

Solution :

2\tan\theta-\cot \theta=-1  \\

2\tan^2\theta+tan\ \theta-1=0 

\left(tan\theta+1\right)\left(2tan\theta-1\right)=0

Now,tan\theta+1=0 or 2tan\theta-1=0

tan\theta=-1=tan\left(\frac{-\pi}{4}\right)or tan\theta=\frac{1}{2\ }=tan\alpha\left(say\right)\\

\theta=n\pi+(\frac{-\pi}{4})\ or\ \theta=n\pi+\alpha,              Where \alpha=\tan^{-1}(\frac{1}{2}) and\ n\in Z

Problem 6: Solve \tan 2 \theta \tan \theta = 1

Solution:

tan\left(2\theta\right)tan\ \theta=1 

\left(\frac{sin\ 2\theta}{cos\ 2\theta}\right)\left(\frac{sin\ \theta}{cos\ \theta}\right)=1 

\left(sin2\theta\right)\left(sin\theta\right)=\left(cos2\theta\right)\left(cos\theta\right) 

cos\ 2\theta cos\ \theta-sin\ 2\theta sin\ \theta=0 cos\left(2\theta+\theta\right)=0 

cos\ 3\theta=0 

3\theta=\left(2n+1\right)\frac{\pi}{2} 

\theta=\left(2n+1\right)\frac{\pi}{6}\ \ or\ \theta=\left(\frac{n\pi}{3}+\frac{\pi}{6}\right)

Problem 7:  Solve \tan (\frac{\pi}{4}+\theta)+\tan (\frac{\pi}{4}-\theta)=4

Solution:

\frac{1+tan\ \theta}{1-tan\ \theta}+\frac{1-tan\ \theta}{1+tan\ \theta}=4 

(1+tan\ \theta)^2+\ (1+tan\ \theta)^2=4(1+tan\ \theta)(1-tan\ \theta)

2+2\ tan^2\theta=4(1+tan\ \theta\ -tan\theta-tan^2\ \theta

2+2\ tan^2\theta=4-4\ tan^2\theta6\ tan^2\theta=2\tan^2\theta=\frac{1}{3}=\ (\frac{1}{\sqrt3})^2=tan^2\frac{\pi}{6}

\theta=n\pi\pm\frac{\pi}{6},\ where\ n\in Z

Problem 8: In \triangle PQR, Prove that 4[bc \cos^2 (\frac{P}{2})+ca \cos^2 (\frac{Q}{2})+ab cos^2 (\frac{R}{2})=(a+b+c)^2

Solution:

L.H.S =

=4[bc(\frac{1+cos\ P}{2})+ca(\frac{1+cos\ Q}{2})+ab(\frac{1+cos\ R}{2}) 

=2\left(bc+ab+bc\right)+2\left(bc c o sP+ca c o sQ+ab c o sR\right)

=2\left(bc+ab+bc\right)+\left(a^2+b^2+c^2\right) 

=(a+b+c)^2

Problem 9: In \triangle PQR, Prove that \frac{1+\cos(P-Q)\cos R}{1+\cos(P-R)\cos Q}=\frac{a^2+b^2}{a^2+c^2}

Solution:

cosR=cos180°-P+Q=-cosP+Q

cos\ Q\ =\ \ cos\ 180°-P+Q=-cosP+Q

=\frac{1+cos\left(P-Q\right)-cos\left(P+Q\right)}{1+cos\ \left(P+R\right)\left\{-cos\left(P+R\right)\right\}}=\frac{1-\left(cos^2P-sin^2Q\right)}{1-\left(cos^2P-sin^2R\right)}

=\frac{\left(1-cos^2P\right)+sin^2Q}{\left(1-cos^2P\right)+sin^2R}=\frac{\sin^2P+sin^2Q}{\sin^2P+sin^2R}

=\frac{\frac{a^2}{K^2}+\frac{b^2}{K^2}}{\frac{a^2}{K^2}+\frac{c^2}{K^2}}=\frac{\frac{a^2+b^2}{K^2}}{\frac{a^2+c^2}{K^2}}

=\frac{a^2+b^2}{a^2+c^2}

Problem 10: Evaluate \tan (\frac{19\pi}{3})

Solution:

tan(2\left(2\pi\right)+\frac{\pi}{3})

=tan\ \frac{\pi}{3}

=\sqrt3

Problem 11: Prove that: Prove that \sin^26x -\sin^2 4x=\sin 2x \sin 10x

Solution:

\sin^26x-\sin^24x

=sin\left(6x+4x\right)sin\left(6x-4x\right)

=sin10xsin2x

Using identity : \sin^2X-\sin^2Y=sin(X+Y)sin(X-Y)

Need some help to solve trigonometry questions?
Hire a Math expert now.

Like this article? Follow us on Facebook and LinkedIn.