Prime Number Program in Java | Prime Checker Java Code

Before jumping into Prime Number Program in Java or how to check whether the given number is prime or not, let’s see what is a Prime number?

In Mathematics a Prime number is defined as a number that has no factors except 1 and the number itself. In other words, a number only divisible by one, and the number itself is called a Prime number.

The Java program for Prime number can be written in several ways. First, let’s try to implement the definition itself.

Prime Number Program in Java – Code

public class PrimeCheck{    
 public static void main(String args[]){    
  int i,flag=0;      
  int n=3;//it is the number to be checked         
  if(n==0||n==1){  
   System.out.println(n+" is not prime number");      
  }else{  
   for(i=2;i<n;i++){ //loop runs for i: 2 -> n-1      
    if(n%i==0){      
     System.out.println(n+" is not prime number");      
     flag=1;      
     break;      
    }      
   }      
   if(flag==0)  { System.out.println(n+" is prime number"); }  
  }//end of else  
}    
}   

OUTPUT

3 is prime number

In the above code, we run a loop from 2 to (n-1) and check if any number divides the given number.

If so then the number is not a Prime number and we set the flag as 1 and terminate the loop with a break statement.
This code works fine. But with the time complexity of O(n). A common idea to reduce this is by running the loop till (n/2). This also works BUT here’s what I think is the best solution for this problem.

BETTER WAY TO CHECK FOR PRIME NUMBER  IN JAVA-

public class PrimeCheck2{    
	public static void main(String args[]){          
		int n=37;//it is the number to be checked    
        if(n == 2 || n == 3 || n ==5 || n == 7) {
        	System.out.println(n +" is a Prime Number!");
        	return;
        }
		if(n%2 != 0 && n%3 != 0 && n%5 != 0 && n%7 != 0)
			System.out.println(n +" is a Prime Number!");
		else
			System.out.println(n +" is not a Prime Number!!");
	}    
}   

OUTPUT

37 is prime number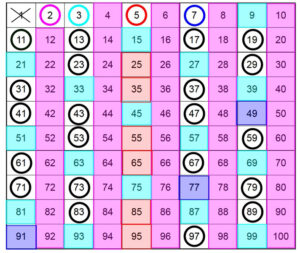

Here we follow the idea that if the given number is 2 or 3 or 5 or 7 then it is prime straight away. Otherwise, we see if the number is not divisible by 2 or 3 or 5 or 7, if so then again it is a Prime or else not. This algorithm is also known as the Sieve of Eratosthenes. All Prime Numbers until a given range can be found using this idea.

Time complexity: O(1) [no iteration required]

Java Program for Prime Numbers using Recursion:

Though not the best way, Prime number check can be a good program to practice recursion and understand its usage. Here we create an IsPrime function with boolean return type- true if Prime: false if not. Here the recursion continues till the divisor i is greater than the square root of the given number.

CODE

public class helloWorld{    
    static boolean isPrime(int n, int i) // call method with i as 2. 
    { 
        // Base cases 
        if (n <= 2) return (n == 2) ? true : false; 
        if (n % i == 0) return false; 
        if (i * i > n) 
            return true; 
       
        // Check for next divisor 
        return isPrime(n, i + 1); 
    } 
	public static void main(String args[]){          
		int n=39;//it is the number to be checked    
        if(isPrime(n, 2)) {
        	System.out.println(n +" is a Prime Number!");
        }
		else
			System.out.println(n +" is not a Prime Number!!");
	}    
}   

OUTPUT

39 is not a Prime Number!!